
The Solution Of The Differential Equation Dy Dx 1 E X Y Is A X Y E X Y 0 B X C E X Y 0 C X C E X Y 1 D X C E X Y 1 0
Thanks for watching like comment and subscribe!Take note we set M as (xy) and N as (xy) in out final answeSolution of the corresponding differential equation 1 y = ex 1 y″ – y′ = 0 2 y = x2 2x C y′ – 2x – 2 = 0 3 y = cos x C y′ sin x = 0 4 y = 1 x2 y′ = 2 1 xy x 5 y = Ax xy′ = y (x ≠ 0) 6 y = x sin x xy′ = y x xy22− (x ≠ 0 and x > y or x < – y) 7 xy = log y C y′ = 2 1 y − xy (xy ≠ 1) 8 y – cos y = x (y sin y cos y x) y′ = y
(1 e^x/y)dx e^x/y(1-x/y)dy=0 exact differential equation
(1 e^x/y)dx e^x/y(1-x/y)dy=0 exact differential equation-X d x ⇒ e y e y 1 d y = − cot x d x Integrating both sides, we get ∫ e y e y 1 d y = − ∫ cot x d x Putting we get Putting e y 1 = t, we getAn "exact" equation is where a firstorder differential equation like this M(x, y)dx N(x, y)dy = 0 has some special function I(x, y) whose partial derivatives can be put in place of M and N like this ∂I∂x dx ∂I∂y dy = 0 and our job is to find that magical function I(x, y) if it exists

1 First Order Ode S 18 03 Exercises 1a Introduction Separation Of Variables
People as Resource MCQ QuestionsSeparating the variables, the given differential equation can be written as 1 e – y d y = x d x ⇒ e y d y = x d x – – – ( i) With the separating the variable technique we must keep the terms d y and d x in the numerators with their respective functions Now integrating both sides of the equation (i), we have ∫ e y d y = ∫ x d x To begin with, we first need to check the exactness of the differential equation dM/dy = 2y, dN/dx = y Now, as the equation is not exact, we need to find out the integration factor that is needed to be adjusted in the equation to make it exact (dM/dy dN/dx) = 2yy = y 1/N{dM/dy dN/dx}=y/(xy)= 1\x Here, we figured that the equation
Solve the differential equation x(y1) dx(x1)dy=0 If y=2 when x=1 Latest Problem Solving in Differential Equations More Questions in Differential Equations Online Questions and Answers in Differential EquationsSteps for Solving Linear Equation y ( x y e ^ { x } ) d x e ^ { x } d y = 0 y ( x y e x) d x − e x d y = 0 Use the distributive property to multiply y by xye^ {x} Use the distributive property to multiply y by x y e x \left (xy^ {2}ye^ {x}\right)dxe^ {x}dy=0 ( x y 2 y e x) d x − e x d y = 0Let's simplify it First dy/dx = (y/x 1)/(y/x 1) Taking y = vx dy/dx = v xdv/dx Therefore, dx/x = (v 1)dv / (v^2 1) Integrating we get log (1/x) logc = arctan (y/x) 1/2 log
(1 e^x/y)dx e^x/y(1-x/y)dy=0 exact differential equationのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 1 | 1 |  1 |
 1 |  1 | 1 |
 1 |  1 |  1 |
「(1 e^x/y)dx e^x/y(1-x/y)dy=0 exact differential equation」の画像ギャラリー、詳細は各画像をクリックしてください。
 1 |  1 |  1 |
1 |  1 | 1 |
 1 | 1 |  1 |
「(1 e^x/y)dx e^x/y(1-x/y)dy=0 exact differential equation」の画像ギャラリー、詳細は各画像をクリックしてください。
 1 |  1 | 1 |
 1 |  1 |  1 |
 1 | 1 | 1 |
「(1 e^x/y)dx e^x/y(1-x/y)dy=0 exact differential equation」の画像ギャラリー、詳細は各画像をクリックしてください。
 1 | 1 |  1 |
1 |  1 |  1 |
 1 |  1 |  1 |
「(1 e^x/y)dx e^x/y(1-x/y)dy=0 exact differential equation」の画像ギャラリー、詳細は各画像をクリックしてください。
1 |  1 |  1 |
 1 | 1 | 1 |
1 |  1 |  1 |
「(1 e^x/y)dx e^x/y(1-x/y)dy=0 exact differential equation」の画像ギャラリー、詳細は各画像をクリックしてください。
 1 |  1 | 1 |
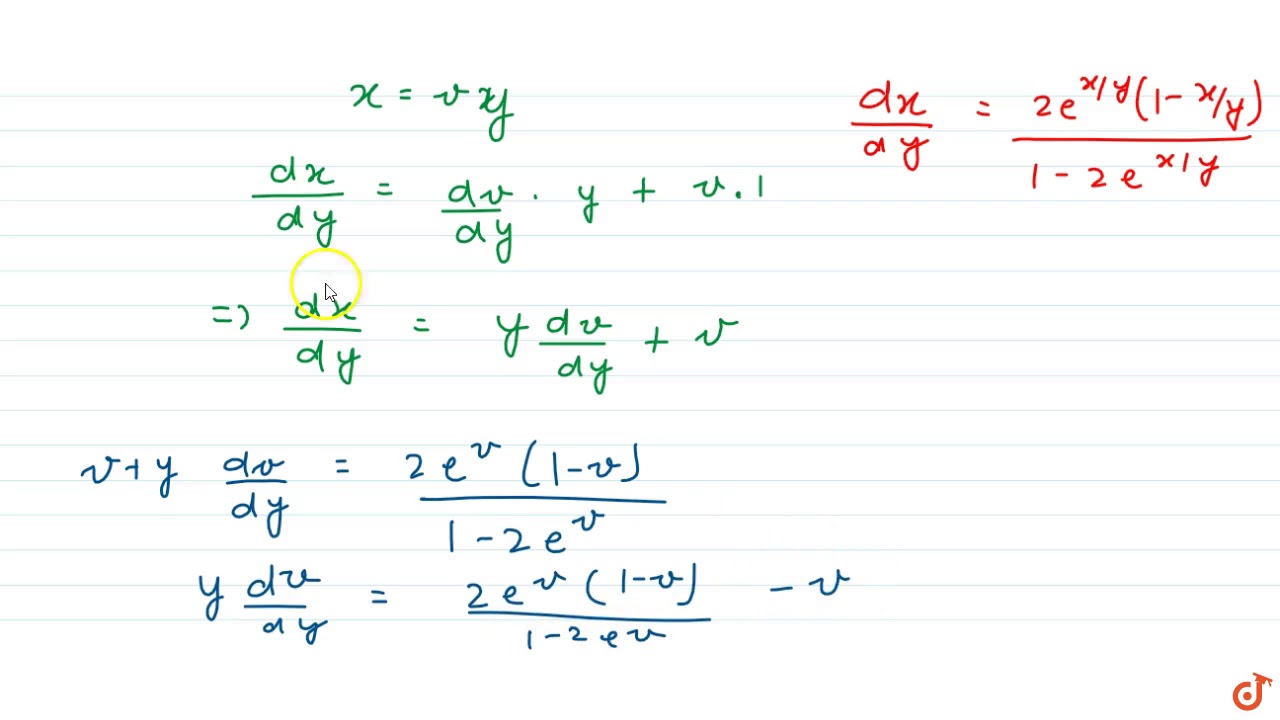 1 |  1 |  1 |
 1 | 1 |  1 |
「(1 e^x/y)dx e^x/y(1-x/y)dy=0 exact differential equation」の画像ギャラリー、詳細は各画像をクリックしてください。
 1 | 1 |  1 |
 1 |  1 | 1 |
1 |  1 | 1 |
「(1 e^x/y)dx e^x/y(1-x/y)dy=0 exact differential equation」の画像ギャラリー、詳細は各画像をクリックしてください。
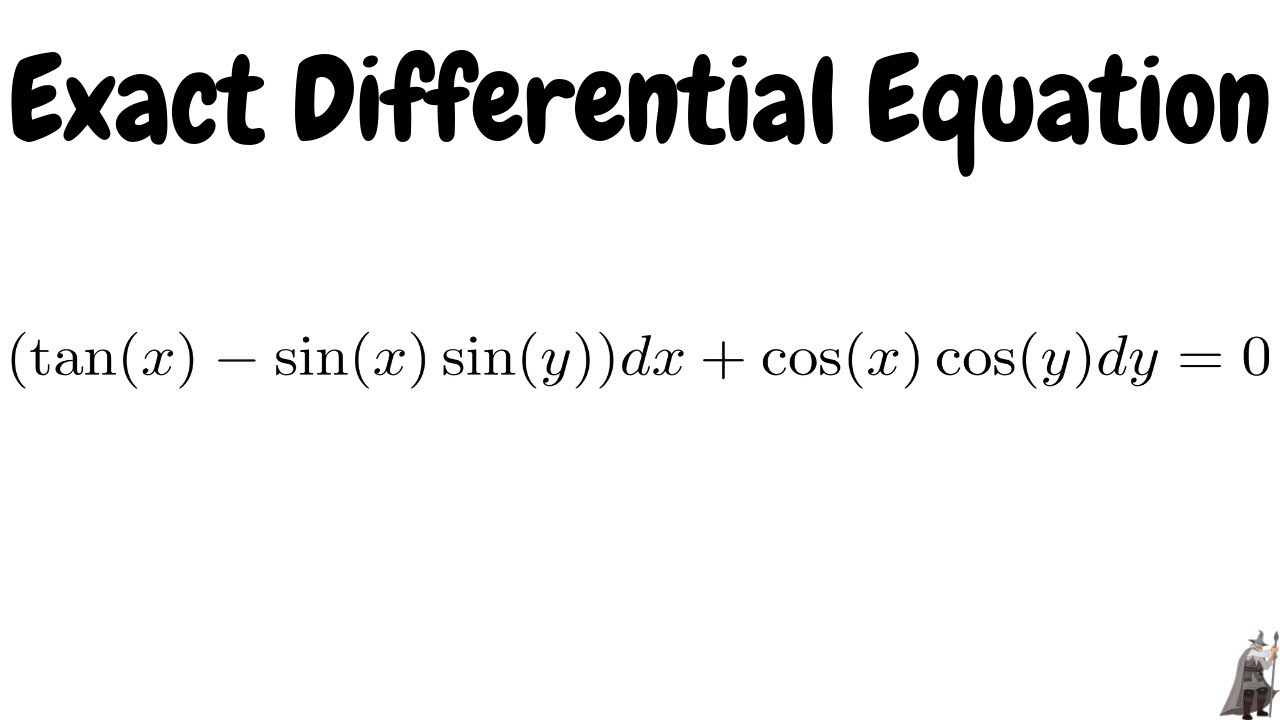 1 |  1 |  1 |
 1 | 1 |  1 |
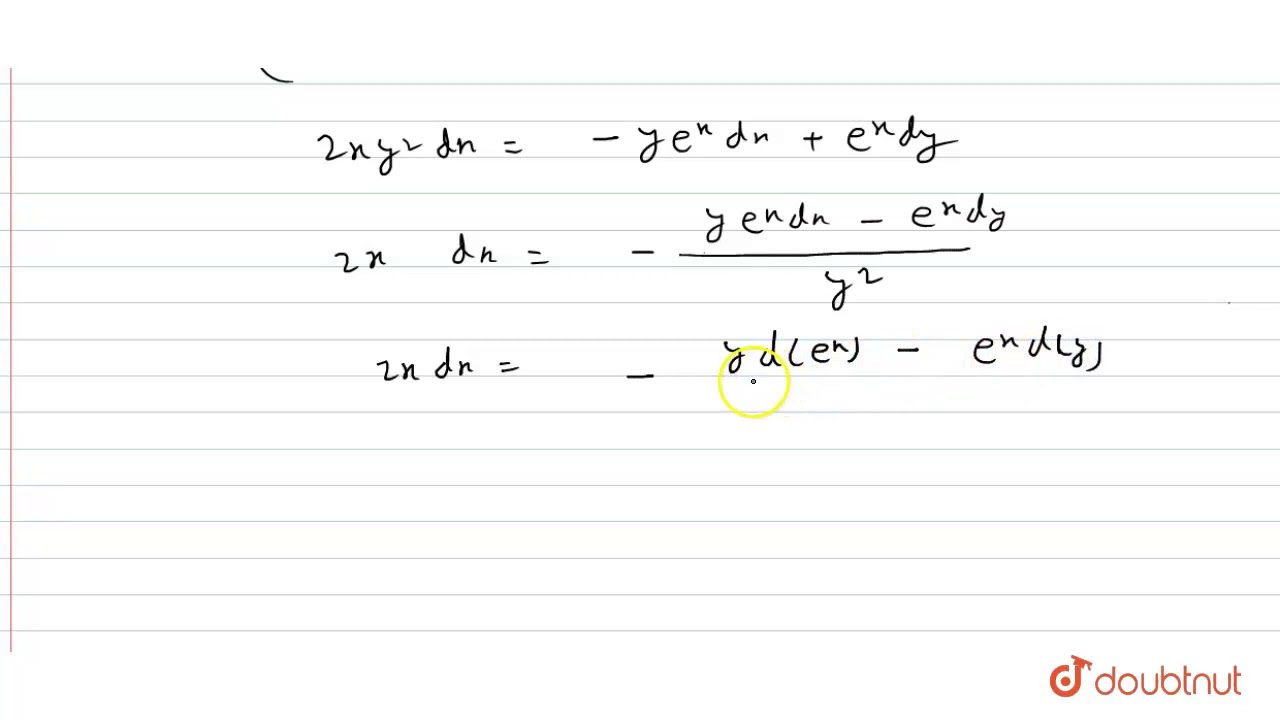 1 |  1 |  1 |
「(1 e^x/y)dx e^x/y(1-x/y)dy=0 exact differential equation」の画像ギャラリー、詳細は各画像をクリックしてください。
1 |  1 |  1 |
1 |  1 |  1 |
 1 |  1 |  1 |
「(1 e^x/y)dx e^x/y(1-x/y)dy=0 exact differential equation」の画像ギャラリー、詳細は各画像をクリックしてください。
 1 |  1 |  1 |
 1 |  1 |  1 |
 1 |  1 | 1 |
「(1 e^x/y)dx e^x/y(1-x/y)dy=0 exact differential equation」の画像ギャラリー、詳細は各画像をクリックしてください。
 1 |  1 |  1 |
 1 |  1 | 1 |
 1 | 1 | 1 |
「(1 e^x/y)dx e^x/y(1-x/y)dy=0 exact differential equation」の画像ギャラリー、詳細は各画像をクリックしてください。
1 |  1 |  1 |
 1 |  1 |
Solve the differential equation dy/dx1/x*y=e^x (dy divide by dx plus 1 divide by x multiply by y equally e to the power of x) various methods for solving and various orders of differential equations THERE'S THE ANSWER! solve the differential equation dy/dx=1e^xy Maths Differential Equations NCERT Solutions;





0 件のコメント:
コメントを投稿