Learn how to solve differential equations problems step by step online Solve the differential equation xy*dx(1x^2)dy=0 Grouping the terms of the differential equation Group the terms of the differential equation Move the terms of the y variable to the left side, and the terms of the x variable to the right side Simplify the expression \frac{1}{y}dy Integrate both sides of the 𝑛 (𝑑^2 𝑦)/(𝑑𝑥^2 ) = 𝐴𝑚2𝑒^(𝑚𝑥 )𝐵𝑛2𝑒^𝑛𝑥 We need to prove (𝑑^2 𝑦)/(𝑑𝑥^2 ) − (𝑚𝑛) 𝑑𝑦/𝑑𝑥 𝑚𝑛𝑦 = 0 Solving LHS (𝑑^2 𝑦)/(𝑑𝑥^2 ) − (𝑚𝑛) 𝑑𝑦/𝑑𝑥 𝑚𝑛𝑦 = (𝐴𝑚2𝑒^(𝑚𝑥 )𝐵𝑛2𝑒^𝑛𝑥) − (𝑚𝑛(b) 2 x y dx ( y 2 x 2) dy = 0 Here, M = 2 x y, M y = 2x, N = y 2 x 2, and N x = 2 xNow, ( N x M y) / M = ( 2 x 2 x ) / ( 2 x y) = 2 / yThus, μ = exp ( ∫ 2 dy / y ) = y2 is an integrating factor The transformed equation is ( 2 x / y ) dx ( 1 x 2 y2) dy = 0 Let m = 2 x / y, and n = 1 x 2 y2Then, m y = 2 x y2 = n x, and the new differential equation is exact

If Y Xx Prove That D2y Dx2 1 Y Dy Dx 2 Y X 0 Explain In Great Detail Mathematics Topperlearning Com X4m0m1ww
Y=x^x prove that d^2y/dx^2-1/y(dy/dx)^2-y/x=0
Y=x^x prove that d^2y/dx^2-1/y(dy/dx)^2-y/x=0-KCET 19 Permutations and Combinations 3 If 2 x 2 y = 2 x y, then d y d x is KCET 4 Let P = a i j be a 3 × 3 matrix and let Q = b i j where b i j = 2 i j a i j for 1 ≤ i, j ≤ If the determinant of P is 2, then the determinant of the matrix Q is IIT JEE 12 Determinants 5Alternative Form of a VariableSeparable Differential Equation Sometimes, a differential equation might be given in the form dy dx = f(y)g(x) d y d x = f ( y) g ( x) Here, we can convert it into



Secure Media Collegeboard Org Digitalservices Pdf Ap Ap16 Calculus Q4 Pdf
1 Multiple by xayb so Mdx Ndy = 0 with M = xayb 1 xa 1yb 2, N = xa 1yb xa 2yb 1 xa 3yb 2 We choose a, b to achieve 0 = ∂yM − ∂xN = (b 1)xayb (b 2)xa 1yb 1 − (a 1)xayb − (a 2)xa 1yb 1 − (a 3)xa 2yb 2 = xayb((b − a)(1 xy) − (a 3)(xy)2) a = b = − 3 So 0 = Mdx Ndy = (x −In calculus, Leibniz's notation, named in honor of the 17thcentury German philosopher and mathematician Gottfried Wilhelm Leibniz, uses the symbols dx and dy to represent infinitely small (or infinitesimal) increments of x and y, respectively, just as Δx and Δy represent finite increments of x and y, respectively Consider y as a function of a variable x, or y = f(x)The differential equation is not well defined in (x,y) = (1,1) as you have an expression of the form 0/0 for dy/dx #8 murshid_islam
Answer to Prove that 2xy\ dx(x^2y^2)\ dy=0 By signing up, you'll get thousands of stepbystep solutions to your homework questions You canSimple and best practice solution for (2xy)dx(x^21)dy=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve itFind dy/dx when x and y are connected by the relation if x = ex/y, prove that dy/dx = xy/x log x asked in Class XII Maths by rahul152 (2,8 points) continuity and differentiability 0 votes 1 answer The degree of the differential equation d2y/dx2 (dy/dx)3 6y5 = 0 is
Click here👆to get an answer to your question ️ dy/dx y^2y1/x^2x1 = 0 prove that (x y 1) = A(1 x y 2xy) where A is parameter parang ganito po yung factor sa, vx (9 x^2 2vx)dx vx ( 6x vx ) dx 9v x^2dx 2 v^2 x^2dx 6vx^2 dx v^2x^2dx (3x^2dv v^2 x^2dx) Picard's Method Picard's Method Consider the first order differential equation dy dx = f(x, y) − − − (1) subject to y(x0) = y0 The equation (1) can be written as dy = f(x, y)dx Integrating between the limits for x and y, we get Dr N B Vyas Numerical Methods Ordinary Differential Equations 60



Does Ay Sin X Y Prove That D 2 Y Dx 2 0 Quora



Rules Of Calculus Functions Of One Variable
Class 12 DifferentiationRD SHARMA EX 112 Q 73 If xy=4, prove that x(dy/dx y^2)=3yDifferentiation Formulas1 d\dx(sin x)=cosx2 d\dx(cos x)=–sinx3 d\dxY=x^x Taking log on both sides log y=log x^x log y=x logx (1/y)(dy/dx)=(x*1/x)logx (dy/dx)=y(1log x) d/dx(dy/dx)=d/dx(y(1logx)) d^2y/dx^2=(1log x)(dy/dx)y/x Now, 1/y(dy/dx)^2=(1/y)*y^2(1logx)^2 Therefore d^2y/dx^21/y(dy/dx)^2y/x=(1log x)dy/dx y(1log x)^2 y/x y/x = (1log x)(1log x) * y y(1log x)^2 =y(1log x)^2 y(1log x)^2Get an answer for 'Q If y=cot x, show that ```(d^2y)/dx^2` 2y `dy/dx` = 0' and find homework help for other Math questions at eNotes



What Is The Solution Of Differential Equation D 2y Dx 2 2 Dy Dx Y 0 When X 0 Y 1 Dy Dx 2 Quora




Engineering Mathematics Notes
COMEDK 08 If y = sin1 ((5x12 √1 x2/13)) , then (dy/dx) = (A) (3/√1 x2) (B) (12/√1 x2) (1/√1 x2) (D) (1/√1 x2) Check ASee the answer dy/dx y/x = x^2*y^2 Best Answer 100% (1 rating) Previous question Next question Get more help from Chegg Solve it with our calculus problem solver and calculator If y x = e yx, prove that dy/dx = (1log y) 2 /log y Related questions 1 vote 1 answer Find dy/dx when x and y are connected by the relation if x = ex/y, prove that dy/dx = xy/x log x asked in Class XII Maths by rahul152 (2,8 points) continuity and differentiability 0



Www Maths Ox Ac Uk System Files Attachments Diffeqs 0 Pdf



Http Www Math Sci Hokudai Ac Jp S Settepanella Teachingfile Calculus Calculus2 Pagine Lineintex Pdf
Thank you for registering One of our academic counsellors will contact you within 1 working day Please check your email for login details Solve the differential equation x(y1) dx(x1)dy=0 If y=2 when x=1 Latest Problem Solving in Differential Equations More Questions in Differential Equations Online Questions and Answers in Differential Equations If log y = tan^1 x, then show that (1 x^2)d^2y/dx^2 (2x 1)dy/dx = 0 asked in Mathematics by Samantha ( 3k points) continuity and differntiability




If X 2 A 2 Y 2 B 2 1 Prove That D 2y Dx 2 B 4 A 2y 3 Brainly In



Http Edshare Soton Ac Uk Id Document 5196
I know that the answer is 4 , in fact the solution given is as follows d 2 x / d y 2 = − ( d 2 y / d x 2) ( d y / d x) − 2 ( d x / d y) = option 4 I don't understand thisFrom where did the minus sign come?Solve 1 and 2 by using separation of variables x^2 dy/dx = y xy;Question Dy/dx Y/x = X^2*y^2 This problem has been solved!




Engineering Mathematics Notes




Higher Engineering Mathematics Bs Grewal Flip Book Pages 501 550 Pubhtml5
if y xx prove that d2y dx2 1 y dy dx 2 y x 0 explain in great detail Mathematics TopperLearningcom x4m0m1ww Starting early can help you score better! Question 28 (OR 1st Question) If √(1−𝑥^2 ) √(1−𝑦^2 ) = a (x − y), then prove that 𝑑𝑦/(𝑑𝑥 ) = √(1 − 𝑦^2 )/√(1 − 𝑥^2 ) Finding 𝒅𝒚/𝒅𝒙 would be complicated here To make life easy, we substitute x = sin A y = sin B (As √(1−𝑥^2 )= √(1−sin^2𝐴 )=√(cos^2𝐴 )) And then solve Let's substitute xHomework Equations The Attempt at a Solution



Secure Media Collegeboard Org Digitalservices Pdf Ap Apcentral Ap15 Calculus Ab Q4 Pdf



Www3 Nd Edu Craicu 1bspring10 Quiz1b Q10 Pdf
The given differential equation is, (1 y 2) dx = (tan 1 y x) dy ⇒ d x d y = 1 1 y 2 ( tan − 1 y − x) ⇒ d x d y x 1 y 2 = tan − 1 y 1 y 2 Now, it is in the standard form of a firstorder linear differential equation Here, P = 1 1 y 2, Q = tan − 1 y 1 y 2Dy dx = f0(x) However, we can treat dy/dx as a fraction and factor out the dx dy = f0(x)dx where dy and dx are called differentialsIfdy/dx can be interpreted as "the slope of a function", then dy is the "rise" and dx is the "run" Another way of looking at it is as follows • dy = the change in y • dx = the change in x Stepbystep explanation Taking log on both sides, Differentiating with respect to x, we have Again differentiating with respect to x, Now, the given equation is = = arrenhasyd and 57 more users found this answer helpful heart outlined



3




Implicit And Logarithmic Differentiation
if y=x^x then prove that d^2y / dx ^ 2 ydy/dx yx=0 Maths Continuity and DifferentiabilityFind dy/dx y^2=(x1)/(x1) Differentiate both sides of the equation Differentiate the left side of the equation Tap for more steps Differentiate using the chain rule, which states that is where and Tap for more steps To apply the Chain Rule, set asInitial Condition y(1) = 1 e^x yy' e^y = e^2x y Remember that you don't have to state the solution as an explicit function of x (ie you don't have to solve your solution for y Question Solve 1 and 2 by using separation of variables x^2 dy/dx = y xy;
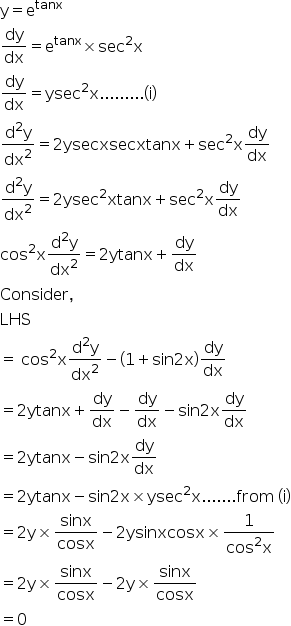



If Y Etan X Prove That Cos2 X D2y Dx2 1 Sin 2x Dy Dx 0 Explain In Great Detail Mathematics Topperlearning Com Mbti5k33




D 2x Dy 2 Equals 1 D 2y Dx 2 1 2 D 2y Dx 2 1 Dy Dx Youtube
if x(1y)^1/2y(1x)^1/2=0 then prove that dy/dx =1/(1x)^2 Share with your friends Share 0 Dear student, murshid_islam said If the boundary condition was , both and would be correct solutions, right?Answered 2 years ago dy/dx=y/ (xsqrt (xy) Divide numerator and denominator with x dy/dx= (y/x)/ (1sqrt (y/x) Consider y=vx dy/dx=vx dv/dx Then Vx dv/ dx=v/ (1sqrtv) xdv/dx




Mathematics Ii Tranquileducation




In Problems 1 10 State Whether The Given Differential Chegg Com
First rearrange the equation x^2\ dyy^2\ dxxy^2(xy)\ dy=0 It can be written as x^2xy^2(xy)\ dy=y^2\ dx \Rightarrow\frac{x^2}{y^2}x^2xy\ dy=dx \Rightarrow \frac{dx}{dyIf y = x^x,then prove thatd^2y dx^2 1 y (dy dx )^2 y x = 0 12th Maths Continuity and Differentiability Logarithmic Differentiation If y = x^x,then prove thatdIf X Y = 1 Prove that D Y D X Y 2 = 0 ?



Www Math Ucla Edu Mt 131a 1 02s 131a Hw Sol Pdf




If Y X X Prove That D 2y Dx 2 1 Y Dy Dx 2 Y X 0
SPECIAL CASE #2 A firstorder differential equation of the form y'=f (axbyc) where b0, can always be reduced to a separable firstorder equation by means of the substitution v=axbyc Example y'=1/ (xy1) Solution If we let v=xy1, then dv/dx=1dy/dx, so the differential equation is transformed into (dv/dx)1=1/v or dv/dx= (1v)/v, soFind dy/dx y^2=1/(1x^2) Differentiate both sides of the equation Differentiate the left side of the equation Tap for more steps Differentiate using the chain rule, which states that is where and Tap for more steps To apply the Chain Rule, set asAlso I don't understand how the above steps are true?



If X Sin T And Y Sin Pt Prove That 1 X2 D2y Dx2 Dy Dx P2y 0 Studyrankersonline




If Y Sin Log X Prove That X2d2y Dx2 Xdy Dx Y 0 Explain In Great Detail Mathematics Topperlearning Com Nwtv8yvv
Homework Statement rewrite the equation in the form of linear equation Then solve it (1x^2)dy/dx xy = 1/ (1x^2) the ans given is y= x/ (1x^2) C / ( sqrt rt (1x^2) ) , my ans is different , which part is wrong ?If `y=x^x ,` prove that `(d^2y)/(dx^2)1/y((dy)/(dx))^2y/x=0` x y = − xy x = − xy −y x = − y ⋅ (x 1) y = − x x 1 dy dx = −1 ⋅ (x 1) − ( −x) ⋅ 1 (x 1)2 dy dx = − 1 (x 1)2 1) I solved this equation for y 2) I differentiated both sides Answer



Www Ualberta Ca Rjia Math215 Hwks Sol1 Pdf




Find The Particular Solution Of The Differential Equation X Y Dy Dx X 2y Given That Y 0 When X 1 Mathematics Shaalaa Com
If x √(1y) y√(1x) = 0, then dy/dx is equal toDy dx =sin5x 2 dx e3x dy =0 3 (x1) dy dx = x6 4 xy0 =4y 5 dy dx = y3 x2 6 dx dy = x2y2 1x 7 dy dx = e3x2y 8 ¡ 4y yx2 ¢ dy − ¡ 2xxy2 ¢ dx =0 9 2y(x1)dy = xdx 10 ylnx dx dy = µ y 1 x ¶ 2 (11) dy dx =sin5x, dy =sin5xdx, Z dy = Z sin5xdx, y = − 1 5 cos5xc, c ∈R (12) dxe3x dyY = x x Applying logarithm, log y = x log x `1/y dy/dx=logxxxx1/x=1logx` `dy/dx=x^x1logx` `(d^2y)/dx^2=(d(x^2))/dx(1logx)x^xd/dx(1logx)` `=x^x(1logx)(1logx)x^x1/x` `=x^x(1logx)^2x^(x1)` `(d^2y)/dx^21/y(dy/dx)^2y/x=x




Implicit Differentiation




If Y Xx Prove That D2y Dx2 1 Y Dy Dx 2 Y X 0 Explain In Great Detail Mathematics Topperlearning Com X4m0m1ww
Solution for 2y (x^2yx)dx (x^22y)dy=0 equation Simplifying 2y (x 2 1y x) * dx (x 2 2y) * dy = 0 Reorder the terms 2y (x x 2 1y) * dx (x 2 2y) * dy = 0 Reorder the terms for easier multiplication 2y * dx (x x 2 1y) (x 2 2y) * dy = 0 Multiply y * dx 2dxy (x x 2 1y) (x 2 2y) * dy = 0 (x * 2dxy x 2 * 2dxy 1y * 2dxy) (x 2 2y) * dy = 0 Reorder the terms (2dxy 2 2dx 2 y 2dx 3 y) (x 2 2y) * dySolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreLet Y be the Laplace Transform of y The derivative of y dy/dx becomes d y/dx = sY y (0) where y (0) is the value of y when x is 0 and the second derivative of y with respect to x d^y/dx^2 becomes d^2 y/dx^2= (s^2)Ys ( y (0)) dy/dx where dy/dx is the value of the first derivative at x =0



5 Derivative Of The Logarithmic Function



Www Amherst Edu Media View Original Ma11spring10finalanswers Pdf
If y = log x √x^21, then prove that (x^2 1)d^2y/dx^2x(dy/dx)=0 asked Mar 13 in Continuity and Differentiability by Tajinderbir ( 370k points) continuity




Homogeneous Differential Equations




Solve Each Differential Equation Dy Dx 5y E 3x Chegg Com




If Y X X Prove That D 2y Dx 2 1 Y Dy Dx 2 Y X 0 Maths Continuity And Differentiability Meritnation Com




The Solution Of The Differential Equation 1 Y X 2y Dx X




Paper




Solve X 2 D 2y Dx 2 X Dy Dx Y 0 Given That Y X 1 X Is A Solution Of It Youtube



Integral Sqrt 1 Dy Dx 2 D 2y Dx 2 Mathematics Stack Exchange



If Xm Yn X Y M N Then Prove That I Dy Dx Y X And Ii D2y Dx2 0 Studyrankersonline




If Y X X Then Prove That D 2y Dx 2 1 Y Dy Dx Y X 0 Youtube



Order And Linearity Of Differential Equations




Implicit Differentiation



Www Math Tamu Edu Glahodny Math442 Solving odes Pdf



Find A Derivative With Step By Step Math Problem Solver



3 8 Implicit Differentiation Calculus Volume 1



Secure Media Collegeboard Org Digitalservices Pdf Ap Ap16 Calculus Q4 Pdf



D Y Dx 2 Zonealarm Results



Http Www Math Sci Hokudai Ac Jp S Settepanella Teachingfile Calculus Calculus2 Pagine Lineintex Pdf




Higher Engineering Mathematics Bs Grewal Flip Book Pages 501 550 Pubhtml5



Www Open Edu Openlearn Ocw Mod Resource View Php Id



How To Solve This Problem 1 X 2 D 2y Dx 2 1 X Dy Dx Y Sin 2log 1 X Quora




What Is The Solution For The Differential Equation Math Frac D 2y Dx 2 Frac Dy Dx 2 Math Quora



Q Tbn And9gctajv1n3e39v2wtv5lp93gqmytgodb4klspgc16k7orbj7klmx5 Usqp Cau



Http Www Cse Salford Ac Uk Physics Gsmcdonald M2 02 Separation Of Variables Pdf




Engineering Mathematics Notes




If Ey X 1 1 Show That D 2y Dx 2 Dy Dx 2 Mathematics Shaalaa Com




If Sec X Y X Y Then D2y Dx2 Mathematics And Statistics Shaalaa Com




Example 17 Show 2y E X Y Dx Y 2x Ex Y Dy 0 Particular
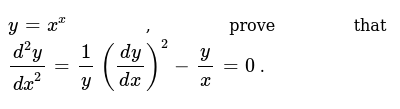



If Y X X Prove That D 2y Dx 2 1 Y Dy Dx 2 Y X 0



Faculty Math Illinois Edu Tyson Existence Pdf



3 8 Implicit Differentiation Calculus Volume 1




Y Ln Y X 2 1 Dy Dx 2xy Y 1 X 2 Y 2 4 Chegg Com



Www Ualberta Ca Csproat Homework Math 334 Assignment solutions Assignment 2 solutions Pdf




W H A T I S D 2 Y D X 2 Zonealarm Results



Http Edshare Soton Ac Uk Id Document 5197



4 2 Implicit Differentiation




Engineering Mathematics Notes




If Y X X Prove That D 2y Dx 2 1 Y Dy Dx 2 Y X 0 Maths Continuity And Differentiability Meritnation Com




Akzxnz3ohhibxm




Solve X 2 D 2y Dx 2 2x Dy Dx 4y X 2 2log X Mathematics 2 Question Answer Collection




Ex 5 7 12 If Y Cos 1 X Find D 2y Dx 2 In Terms Of Y Alone



Projecteuclid Org Download Pdf 1 Euclid Jdg




If Y X X Find D 2y Dx 2



1




If X Logt And Y 1 T Prove That D2y Dx2 Dy Dx 0 Brainly In



Scholarspace Manoa Hawaii Edu Bitstream Differentialequations Pdf




Solve X D 2 Dx 2 2x 1 Dy Dx X 1 Y 0 Given That Y E X Is An Integral Included In The Complementary Function सम करण X D 2 Dx 2 2x 1 Dy Dx X 1 Y 0 क हल क ज ए द य गय ह क Y E X



Secure Media Collegeboard Org Digitalservices Pdf Ap Ap16 Calculus Q4 Pdf



Http Www Stat Wisc Edu Ifischer Calculus Pdf




If X Sint Y Sinmt Prove That 1 X 2 D 2y Dx 2 X Dy Dx M 2 Y 0 Maths Continuity And Differentiability Meritnation Com



For A Function Y F X Then Prove That 1 Dy Dx 2 3 2 D 2y Dx 2 1 Dx Dy 2 3 2 D 2x Dy 2 0 Sarthaks Econnect Largest Online Education Community




Worked Example Identifying Separable Equations Video Khan Academy



Www Tau Ac Il Levant Ode Solution 6 Pdf




If X 2 A 2 Y 2 B 2 1 Prove That D 2y Dx 2 B 4 A 2 Y 3 Youtube



Users Math Msu Edu Users Gnagy Teaching 10 Fall Mth234 W6 234 H Pdf



If Y X X Prove That D 2y Dx 2 1 Y Dy Dx 2 Y X 0 Sarthaks Econnect Largest Online Education Community



Q Tbn And9gcq69xqaiwgxy95 44f5sqsm2pnlgxvor Roue6xadfczqpkv4qx Usqp Cau



4 2 Implicit Differentiation



If Y X X Prove That D 2y Dx 2 1 Y Dy Dx 2 Y X 0 Sarthaks Econnect Largest Online Education Community




If X 1 Y 2 Y 1 X 2 1 Prove That Dydx 1 Y 2 1 X 2



If Yx Ey X Prove That Dy Dx 1 Log Y 2 Log Y Studyrankersonline




If Y Cos M Cos 1 X Show That 1 X 2 Y X Y M 2 Y 0




If X 1 Y Y 1 X 0 Then Prove That 1 X 2 Dydx 1 0




Engineering Mathematics Ii Pages 151 0 Flip Pdf Download Fliphtml5




If Y X X Prove That D 2y Dx 2 1 Y Dy Dx 2 Y X 0 Brainly In



Scholarspace Manoa Hawaii Edu Bitstream Differentialequations Pdf



Implicit Differentiation



Canvas Harvard Edu Courses 376 Files 54 Download Verifier De5arviftgyjwzvw3gibhrarwdtqtzfkmagbtegv




Pdf Complete Solutions Differential Equations With Modeling Applications Differential Equations With Boundary Value Problems 5th Edition Juan Carlos Becerra Linares Academia Edu



Www Utdallas Edu Efrom Solhw Pdf




W H A T I S D 2 Y D X 2 Zonealarm Results




Show That Z Ln X 2 Y 2 2 Tan 1 Y X Satisfies The Laplaces S Equation Mathematics Stack Exchange
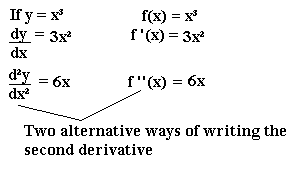



The Second Derivative Mathematics A Level Revision




Second Derivatives Implicit Equations Find Expression Video Khan Academy
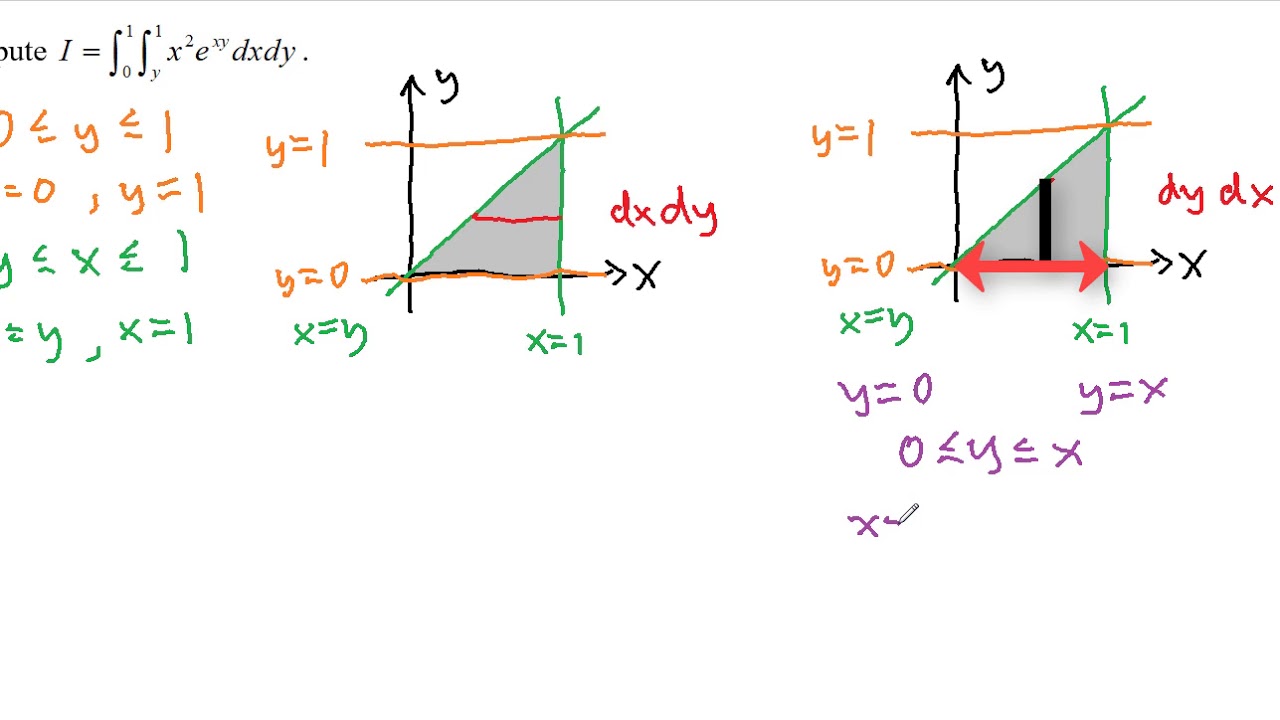



Double Integrals Volume And Average Value




Engineering Mathematics Notes




Worked Example Implicit Differentiation Video Khan Academy



0 件のコメント:
コメントを投稿